Support Vektor Maschinen (SVM)

Support Vector Maschinen sind eine praktische Möglichkeit zur Klassifizierung von multidimensionalen Daten, speziell wenn diese sich nicht sauber durch das Setzen eines Threshold separieren lassen. [1] Das Konzept der Support Vektoren 1-dimensionale Daten: Wenn nur eine zu messende Charakteristik betrachtet wird, zum Beispiel wenn jedes in dieser Arbeit betrachtete Support Ticket nur genau eine Kategorie haben kann, dann können diese Daten auf einer Geraden dargestellt werden. Der
Threshold wird hier als Punkt dargestellt beziehungsweise als Linie auf jener Geraden. Abbildung 1 stellt dies beispielhaft dar. Hier erlaubt man jedoch immer nur die Prüfung der Daten auf eine Eigenschaft, die Zugehörigkeit zu der soeben betrachteten Klasse zum Beispiel. Bei mehreren Klassen müsste man immer wieder neue Durchläufe starten, wenn man im eindimensionalen Raum bleiben möchte.

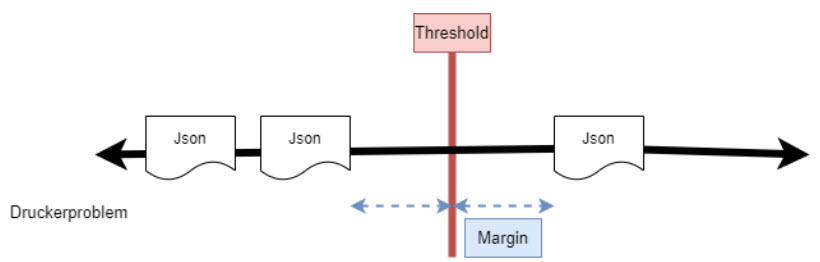
Abbildung 1: 1-dimensionale Daten getrennt durch Threshold, Maximal Margin Classifier

Das Problem ist hier nun, dass die Daten sehr genau in die zwei Kategorien fallen müssen, wie im Beispiel hier: „Inhalt der JSON-Datei ist ein Druckerproblem, oder Inhalt der JSON-Datei ist kein Druckerproblem“. Mit Ausreißern in den Messungen, zum Beispiel der Text beschäftigt sich mit Druckern, aber nicht mit Defekten, sondern mit einem Neukauf und wäre also eigentlich der Kategorie „Einkauf“ zuzuordnen, kann hier nicht umgegangen werden. Diese Eingaben können falsch positive bzw. falsch negative Ergebnisse erzielen.
Wenn man diese falschen Klassifizierungen jedoch zulässt und das Konzept der Soft-Margins einsetzt, dann lässt sich das Verhältnis zwischen richtig und falsch kategorisierten Daten optimieren. Soft-Margins sind die Abstände von Messpunkten, hier als Beispiel Dokumente auf der Geraden, zum Threshold, jedoch nicht nur jenen an den äußersten Rändern der Cluster,
sondern von jedem getätigten Messpunkt. In der Mitte, zwischen solchen Messpunkten, wird der Threshold gesetzt. Somit ergeben sich mehrere mögliche Threshold Werte. Um den Optimalen festzustellen kann man Kreuzvalidierung (Cross-Validation) einsetzen. Hier betrachtet man welcher Threshold-Wert genau wie viele falsche und richtige Klassifizierungen ergibt. Jene Kombination aus Soft-Margin/Threshold mit den meisten richtigen Klassifizierungen, stellt den besten Wert dar. Messungen innerhalb des Soft-Margin und am Rand des Clusters sind die Support Vektoren. Abbildung 2 veranschaulicht die bis jetzt vorgestellten Konzepte:

Abbildung 2: SV Klassifizierung, 1-dimensional, mit Soft-Margins, Ausreißer und falschem Negativum

Das Konzept der Hyperplanes und Support Vektor Maschinen

Je nach der Dimensionalität der Daten werden die Support Vektoren unterschiedlich dargestellt. 1-dimensionale Daten (wie im Beispiel oben) haben einen Support Vektor der als Punkt, bzw. Linie dargestellt werden kann (Siehe Abbildung 5). 2-dimensionale Daten, welche auf einer X und Y Koordinate aufgetragen werden können, als 1-dimensionale Gerade dargestellt werden, 3-dimensionale Daten, aufgetragen auf X, Y und Z Koordinate ergeben dagegen eine 2-dimensionale Fläche als Support Vektor.
Es gibt aber auch n-dimensionale Daten, wobei n-dimensionale Daten generell nur mehr als Hyperplane bezeichnet werden. Im Gegensatz zu den vorher genannten Beispielen, welche sich noch graphisch darstellen lassen, stößt man bei Dimensionen größer als 3 an die Grenzen der grafischen Darstellung. Die Klassifizierung, welche im Zuge dieser Bachelorarbeit durchgeführt wird, beschäftigt sich genau mit solchen n-Dimensionalen Daten. Ein JSON-Dokument kann gleichzeitig ein Druckerproblem beschreiben, ein Ticket für den Einkauf sein, und beschäftigt sich
zusätzlich noch mit der Ausstattung für einen neuen Arbeitsplatz. Hinzu kommt noch eine Priorität (welche ja auch eine Klasse ist), was die Anzahl der Dimensionen auf 4 erhöht.

Support Vektor Maschinen

Die bis jetzt vorgestellten Konzepte können bereits mit einigen Szenarien wie
ungewöhnlichen Messergebnissen (Ausreißer), falschen Klassifizierungen und überlappenden Kategorien umgehen, jedoch stoßen Support Vector Classifier an ihre Grenzen, wenn Daten nicht genau in zwei Kategorien geteilt werden können, durch die Trennung mittels Threshold, sondern vielmehr in einen Bereich fallen, welcher flankiert von anderen Klassen ist. In Abbildung 3 wird dies mit einem kurzen Gedankenexperiment dargelegt.

Hier sieht man nochmals die 1-dimensionale Darstellung von Tickets mit Druckerproblemen, dargestellt als eine fiktive Prozentanzahl der Wahrscheinlichkeit, dass das betrachtete JSON-File wirklich ein Druckerproblem ist, gepaart mit einem Multiplikator für die Priorität des Tickets. Wobei nur solche Tickets echte Druckerprobleme sind (Hardware, Toner etc.) welche in einen Mittelbereich fallen. Tickets it zu hohen Werten (Priorität Kritisch) und jene mit zu niedrigen Werten (Priorität Low) sind keine echten Druckerproblemtickets. Es gäbe also 2 Thresholds.

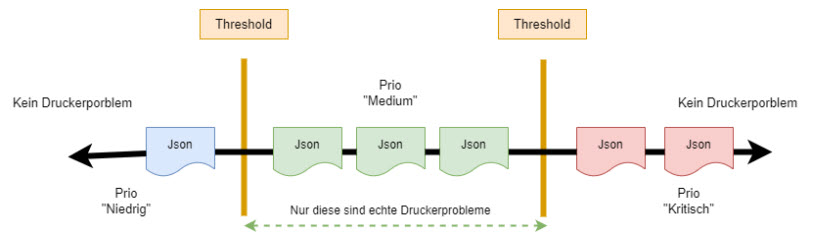
Abbildung 3: Problem mit Bereichsdaten, wo greift der Threshold?

Hier liegt der Vorteil von SVMs. Sie transformieren niedrigdimensionale Daten in höhere Dimensionen. Dabei ist zu bedenken, dass Kategorien zuvor in Zahlenwerte überführt werden müssen, um mathematisch transformiert werden zu können.
Um beim 1-dimensionalen Beispiel in Abbildung 3 zu bleiben: Wenn also die JSON-Dokumente mithilfe von Zahlwerten klassifiziert wurden (Zum Beispiel die Wahrscheinlichkeit in % mit der sie zur Klasse Druckerproblem gehören, multipliziert mit einem Faktor für die Priorität des Tickets, dann könnte man mithilfe der Support Vektor Maschine die Daten in die 2. Dimension überführen. Der Threshold wäre dann eine 1- dimensionale Gerade zwischen diesen Werten. Abbildung 4 zeigt eine solche Transformation beispielhaft:

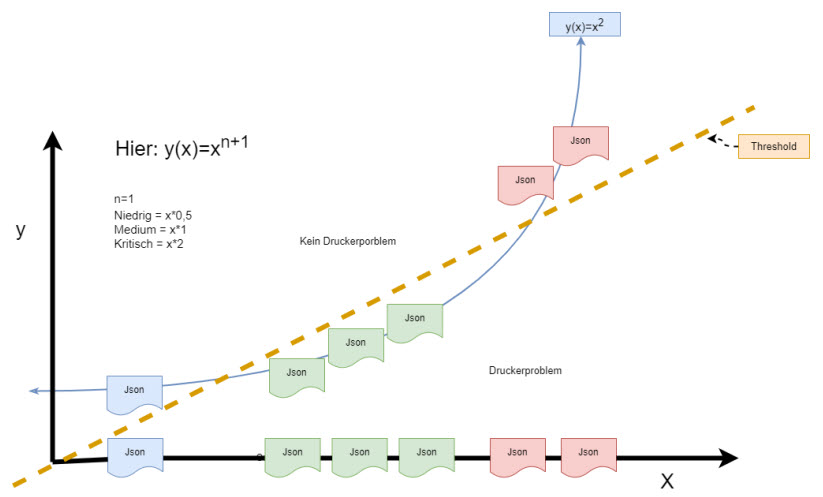
Abbildung 4: Darstellung der Transformation in höhere Dimension durch SVM

Somit können neue Messungen, die in den grünen Mittelbereich fallen, wo also der Text zu einem gewissen Prozentsatz etwas mit Druckern zu tun hat und die eine Priorität Medium war, abgegrenzt werden von jenen am linken und rechten Ende des Spektrums und eine Klassifizierung kann wieder durchgeführt werden, da der Threshold wieder die Daten richtig abgrenzt. [2]
Scikit-Learn beherrscht mit seinen Polynomial-Kernel- und Radial-Kernel-Funktionen alle nötigen Tools, um Support Vektoren im n-dimensionalen Raum zu berechnen. Diese Funktionen werden benötigt, um herauszufinden mit welchem Wert die anderen Achswerte faktorisiert werden müssen, um den zusätzlichen Achswert (Y in Abbildung 4) zu erhalten und wird in der Praxis häufig verwendet. Dieser Artikel versucht jedoch das zugrundeliegende Prinzip zu erklären und mit einem Praktischen Beispiel die Arbeit mit Dimensionalität von Daten zu veranschaulichen.